- Clustering
- unsupervised learning, without response variable
- Hierarchial Clustering
head(USArrests)## Murder Assault UrbanPop Rape
## Alabama 13.2 236 58 21.2
## Alaska 10.0 263 48 44.5
## Arizona 8.1 294 80 31.0
## Arkansas 8.8 190 50 19.5
## California 9.0 276 91 40.6
## Colorado 7.9 204 78 38.7zUSArrests = scale(USArrests)
summary(zUSArrests)## Murder Assault UrbanPop Rape
## Min. :-1.6044 Min. :-1.5090 Min. :-2.31714 Min. :-1.4874
## 1st Qu.:-0.8525 1st Qu.:-0.7411 1st Qu.:-0.76271 1st Qu.:-0.6574
## Median :-0.1235 Median :-0.1411 Median : 0.03178 Median :-0.1209
## Mean : 0.0000 Mean : 0.0000 Mean : 0.00000 Mean : 0.0000
## 3rd Qu.: 0.7949 3rd Qu.: 0.9388 3rd Qu.: 0.84354 3rd Qu.: 0.5277
## Max. : 2.2069 Max. : 1.9948 Max. : 1.75892 Max. : 2.6444Clustering - average clustering with 5 rectangels
#Using average
hc1 = hclust(dist(zUSArrests),method="average")
plot(hc1,hang=-1)
rect.hclust(hc1,k=5)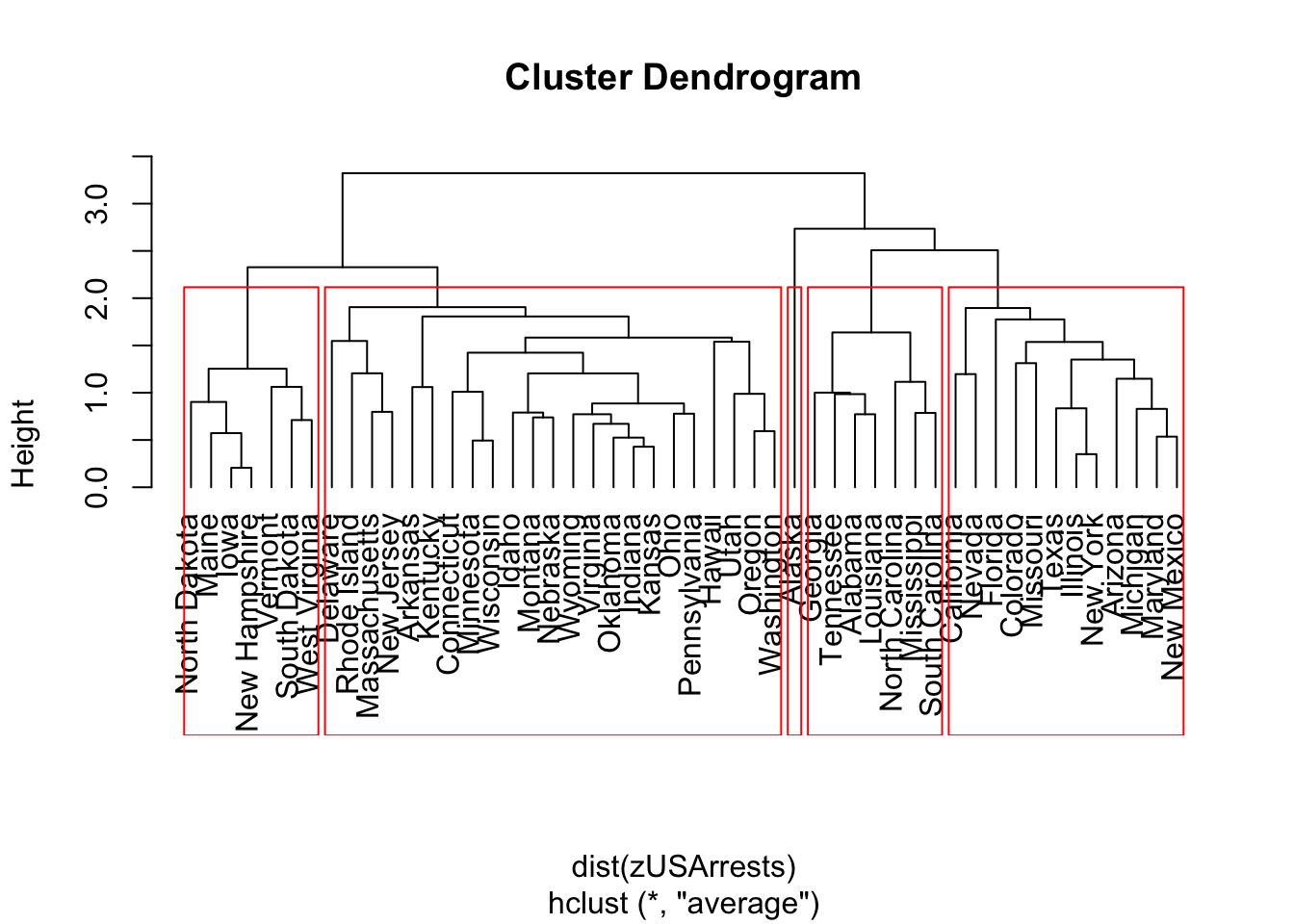
Show the clusters
cutree(hc1,k=5)## Alabama Alaska Arizona Arkansas California
## 1 2 3 4 3
## Colorado Connecticut Delaware Florida Georgia
## 3 4 4 3 1
## Hawaii Idaho Illinois Indiana Iowa
## 4 4 3 4 5
## Kansas Kentucky Louisiana Maine Maryland
## 4 4 1 5 3
## Massachusetts Michigan Minnesota Mississippi Missouri
## 4 3 4 1 3
## Montana Nebraska Nevada New Hampshire New Jersey
## 4 4 3 5 4
## New Mexico New York North Carolina North Dakota Ohio
## 3 3 1 5 4
## Oklahoma Oregon Pennsylvania Rhode Island South Carolina
## 4 4 4 4 1
## South Dakota Tennessee Texas Utah Vermont
## 5 1 3 4 5
## Virginia Washington West Virginia Wisconsin Wyoming
## 4 4 5 4 4Center points for each cluster
cluster <- cutree(hc1,k=5)
cent <- NULL
for (k in 1:5){
cent <- rbind(cent, colMeans(USArrests[cluster == k,]))
}
cent## Murder Assault UrbanPop Rape
## [1,] 14.671429 251.28571 54.28571 21.685714
## [2,] 10.000000 263.00000 48.00000 44.500000
## [3,] 10.883333 256.91667 78.33333 32.250000
## [4,] 5.530435 129.43478 68.91304 17.786957
## [5,] 2.700000 65.14286 46.28571 9.885714- K-means Clustering
# 4 clusters
kmc1 = kmeans(zUSArrests,4)
kmc1## K-means clustering with 4 clusters of sizes 10, 20, 10, 10
##
## Cluster means:
## Murder Assault UrbanPop Rape
## 1 -0.2084716 -0.4110987 -0.3412836 -0.2030666
## 2 1.0049340 1.0138274 0.1975853 0.8469650
## 3 -0.6286291 -0.4086988 0.9506200 -0.3888373
## 4 -1.1727674 -1.2078573 -1.0045069 -1.1020261
##
## Clustering vector:
## Alabama Alaska Arizona Arkansas California
## 2 2 2 1 2
## Colorado Connecticut Delaware Florida Georgia
## 2 3 3 2 2
## Hawaii Idaho Illinois Indiana Iowa
## 3 4 2 1 4
## Kansas Kentucky Louisiana Maine Maryland
## 1 1 2 4 2
## Massachusetts Michigan Minnesota Mississippi Missouri
## 3 2 4 2 2
## Montana Nebraska Nevada New Hampshire New Jersey
## 1 1 2 4 3
## New Mexico New York North Carolina North Dakota Ohio
## 2 2 2 4 3
## Oklahoma Oregon Pennsylvania Rhode Island South Carolina
## 1 1 3 3 2
## South Dakota Tennessee Texas Utah Vermont
## 4 2 2 3 4
## Virginia Washington West Virginia Wisconsin Wyoming
## 1 3 4 4 1
##
## Within cluster sum of squares by cluster:
## [1] 6.148786 46.747955 9.326266 7.443899
## (between_SS / total_SS = 64.5 %)
##
## Available components:
##
## [1] "cluster" "centers" "totss" "withinss" "tot.withinss"
## [6] "betweenss" "size" "iter" "ifault"Scatterplot
pairs(zUSArrests,col=kmc1$cluster, pch=16)
Elbow Point - chooses k where plot harshly drops - in this case, k = 4
wss = 0
for (i in 1:10) {wss[i]=sum(kmeans(zUSArrests,center=i)$withinss)}
plot(1:10,wss,type='b',xlab='Number of Clusters',ylab='Within group sum of squares')
- K-medoid Clustering
library(fpc)
kmed = pamk(zUSArrests,4)
kmed## $pamobject
## Medoids:
## ID Murder Assault UrbanPop Rape
## Alabama 1 1.2425641 0.7828393 -0.5209066 -0.003416473
## Michigan 22 0.9900104 1.0108275 0.5844655 1.480613993
## Oklahoma 36 -0.2727580 -0.2371077 0.1699510 -0.131534211
## New Hampshire 29 -1.3059321 -1.3650491 -0.6590781 -1.252564419
## Clustering vector:
## Alabama Alaska Arizona Arkansas California
## 1 2 2 1 2
## Colorado Connecticut Delaware Florida Georgia
## 2 3 3 2 1
## Hawaii Idaho Illinois Indiana Iowa
## 3 4 2 3 4
## Kansas Kentucky Louisiana Maine Maryland
## 3 3 1 4 2
## Massachusetts Michigan Minnesota Mississippi Missouri
## 3 2 4 1 3
## Montana Nebraska Nevada New Hampshire New Jersey
## 3 3 2 4 3
## New Mexico New York North Carolina North Dakota Ohio
## 2 2 1 4 3
## Oklahoma Oregon Pennsylvania Rhode Island South Carolina
## 3 3 3 3 1
## South Dakota Tennessee Texas Utah Vermont
## 4 1 2 3 4
## Virginia Washington West Virginia Wisconsin Wyoming
## 3 3 4 4 3
## Objective function:
## build swap
## 1.035116 1.027102
##
## Available components:
## [1] "medoids" "id.med" "clustering" "objective" "isolation"
## [6] "clusinfo" "silinfo" "diss" "call" "data"
##
## $nc
## [1] 4
##
## $crit
## [1] 0.0000000 0.0000000 0.0000000 0.3389904